□がある式を線分図で描かせよう!(一年生。中学受験のみ)
かんたんな足し算や引き算で線分図を描けるようになれば、「2+□=5」のような□がある式を、線分図で表せるようにしましょう。
ただ、□は変数です。
小学生の範囲から逸脱していますし、一年生に教える必要性はあまりないので、中学受験を考えていなければ教える必要はありません。
中学受験を考えていて、かつ、先取り学習したいひとのみ、教えるといいでしょう。
というわけで、□がある場合の線分図ですが、ここではつぎの4つの線分図の描きかたを説明しています。
・2+□=5
・8−□=3
・□+2=8
・□−2=5
「かんたんじゃないの?」
大人はそう思ってしまいますが、一年生だと、まだ脳が育っておらず変数という抽象概念を理解できない、すなわち、□がある場合の線分図を何度教えても理解できないことがあります。
逆をいえば、脳の発達を待てば、かんたんに理解できるので、どうしても子どもが理解しない場合は、二年生、三年生になってから教えるといいでしょう。
スポンサード リンク
2+□=5 の線分図の描きかた
まずは「2+3」の線分図を描かせてください。
前のページでしっかり練習していれば、描けると思います。
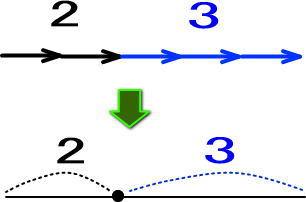
上図を指し示しながら「2あった。それに3を足したんだよね」と言ってください。
そして、つぎのように言ってください。
「2あった。それに4を足せば、どうなると思う? 線分図で描いてみて」
「2あった。それに5を足せば、どうなると思う? 線分図で描いてみて」
「2あった。それに6を足せば、どうなると思う? 線分図で描いてみて」
つぎのようになりますね。
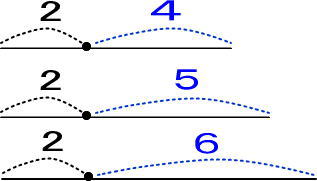
ここからが本番です。
「じゃあ、2あった。□を足した場合を線分図にしてみて」と言ってください。
はじめはポカンとした顔をすると思います。
そこで、2に4を足した場合、2に5を足した場合、2に6を足した場合の線分図を指さしながら、「どこが変わっている? 見比べて」と言ってください。
そして「青いところだよね」と言いつつ「□を足したわけだから、つぎのようになるんだ」と教えてあげてください。

これで、「わかる」子どもは少ないと思います。
しかし「できる」子どもはいます。
「ワケがわかっていなさそうだけど、できそうだな」と思えば、このまま一気に先に進めてください。
「できなさそう」と思えば、無理する必要はありません。ここは先送りにしましょう。
(問)「4+□」を線分図にしてみましょう。
「4あった。それに□を足した」わけなので、つぎの図になります。

ここまでできれば、「2+□=5」も線分図で描けると思います。
子どもに線分図を描かせてみましょう!
2+□の線分図はわかりますよね。
これが5なので、つぎのようになります。
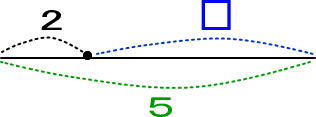
(問)4+□=7 を線分図で描かせてみましょう!
4+□の線分図はわかりますよね。
これが7なので、つぎのようになります。
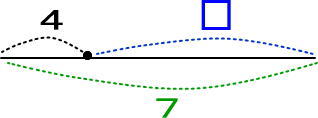
あとは、たとえば「7+□=10」のように数字を変えて、繰り返し線分図を描かせるといいでしょう。
なお、この時点では「わからないけど、できる」の子どもがたいはんだと思います。
繰り返し、線分図を描かせることで「なんとなくわかる」ようになるので、何度も線分図を描かせましょう。
【目標】2+□=5のような式を線分図にできる
スポンサード リンク
8−□=3 の線分図の描きかた
まずは「8−7」の線分図を描かせてください。
前のページでしっかり練習していれば、描けると思います。
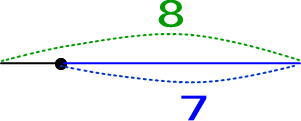
上図を指し示しながら「8あった。そこから7を引いたんだよね。だから、いま、この青い部分なはいよね」と言ってください。
そして、つぎのように言ってください。
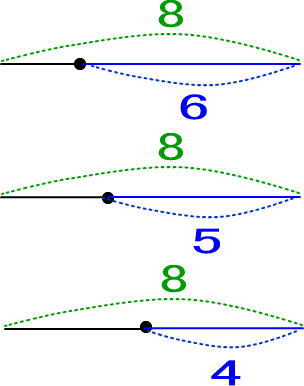
「8あった。そこから6を引けば、どうなると思う? 線分図で描いてみて」
「8あった。そこから5を引けば、どうなると思う? 線分図で描いてみて」
「8あった。そこから4を引けば、どうなると思う? 線分図で描いてみて」
つぎのようになりますね。
ここからが本番です。
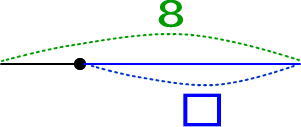
「じゃあ、8あった。そこから□を引けば、どうなると思う? 線分図にしてみて」と言ってください。
先ほどの足し算がわかっていれば、すんなり描くと思います。
もしわからなさそうにしていれば、先ほどと同様に、8から6を引いた場合、8から5を引いた場合、8から4を引いた場合の線分図を指さしながら、「どこが変わっている? 見比べて」と言ってください。
そして「青いところだよね」と言いつつ「□を引いたわけだから、つぎのようになるんだ」と教えてあげてください。
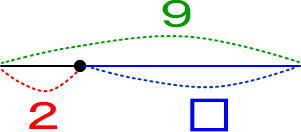
(問)9−□=2 を線分図で描かせてみましょう!
9−□の線分図は描けると思います。
あとは、どこが2なのか、子どもに教える必要があります。
まずは、9−□の線分図を描かせてください。
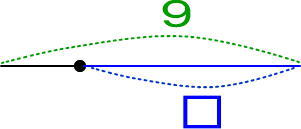
「9から□を引いたということは、9から□をとったわけだよね。残りはどこ?」と聞いてください。
わからないようなら、「9の長さのひもがあったとするね。そこから□だけ引くということは、□の長さだけ、チョキンと切ったってこと。残っているのはどこ?」と聞いてください。
「青いところ」と気がつくと思います。
「そこが2とあるよね。だから、このようになるんだ」と教えてください。
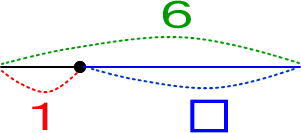
(問)6−□=1 を線分図で描かせてみましょう。
つぎのようになります。
あとは、たとえば「9−□=2」のように数字を変えて、何度も線分図を描かせましょう。
【目標】8−□=5のような式を線分図にできる