かけ算は「コピー機」とイメージしよう！

りんご２個を３回コピーしてみよう！

りんごが２個あったとします。
これをコピー機で３回コピーしたとしましょう。
コピー機から出てくる、りんごは何個になりますか。
※もとのりんごは原本なので、コピー機からでてきませんよね。だから、元のりんごは除外します。

つぎの図をみれば、合計６個になることがわかります。

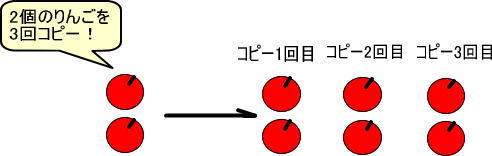
これが、かけ算のイメージです。

「▲×●」を見れば、つぎのように考えるといいでしょう。

・「▲」は「りんご▲個」
・「×●」は「●回コピーする」

ちなみに、当サイトの子ども向けの算数のページでは、「ハンコ」で教えていますが、ハンコでもコピー機でもどちらでも構いません。
小さな子どもは「ハンコは馴染みがある。コピー機が何かわからない」ですが、大人は「コピー機のほうが馴染みがある」から、そうしているだけです。

スポンサードリンク

「図を描いて」、かけ算の計算をしてみよう！

「３×４」を計算してみましょう。
即座に答えがわかると思いますが、「イメージ」することが大切です。
コピー機の図を描いて計算してみましょう！

さて、「３×４」の「３」は「りんご３個」、「×４」は「４回コピーする」と考えます。
つまり「りんご３個を４回コピーする」となります。
よって、つぎの図のようになります。

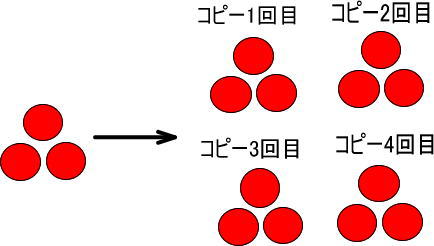
りんごを数えると、「１２」だとわかります。
よって、「３×４＝１２」です。

スポンサードリンク

かんたんな方程式なら解ける！

「なぜ、コピー機とイメージしないといけないのか」と思っているかたに向けて、方程式の考え方を紹介します。
※方程式については、今後、詳しく解説します。「さわり」の部分だけです。

「〇×３＝９」の〇はいくつだと思いますか。

みなさんは、すでに方程式を学習しているので、「〇＝９÷３＝３」とわかると思います。
しかし、なぜそのように計算になるのかまで説明できない、イメージできないのではないでしょうか。
そこで、「コピー機」がでてきます。

さて、「×３」は「３回コピーする」という意味でした。よって、「〇×３」は、「〇を３回コピーする」という意味になります。
これを図で表すと、つぎのようになります。

〇はすべてコピーしたものなので、ぜんぶ、まったく同じものですよね。

つまり、もし１つの〇の正体が「１」であれば、ほかの〇もすべて「１」になるはずです。

１が３つあるので、数えると、ぜんぶで「３」になります。
ここで問題文をもう一度よく読んでみてください。
「〇×３＝９」と、すなわち、ぜんぶで「９」とあるので、〇は１ではありません。

つぎに、もし１つの〇の正体が「２」であれば、どうでしょうか。
ほかの〇もすべて「２」になります。

２が３つあるので、数えると「６」ですね。
「〇×３＝９」とあるので、〇は２ではありません。

つぎに、もし１つの〇の正体が「３」であれば、どうでしょうか。
ほかの〇もすべて「３」になります。

３が３つあるので、数えると「９」です。
「〇×３＝９」とあるので、〇は３です。

ここからが本番です。
コピー機のイメージがあれば、同類項のたし算、ひき算も、かんたんに理解できます。

同類項のたし算、ひき算も、かんたんに理解できる！

つぎは「〇×２＋〇×３＝１５」を解いてください。

先ほどと比べて難しくなっていますが、何が難しいのかというと「＋」ではないでしょうか。

この「＋」はどういう意味でしょうか。
それを考えるために、つぎの２つの図を描いてみてください。

１．「３×２」をコピー機の図で表す
２．「３×３」をコピー機の図で表す

「３」はりんご３個です。
「×２」「×３」はそれぞれ「２回コピー」「３回コピー」ですね。
よって、つぎの図になります。

さて、ここでもう一度、上図を見てください。
四角で囲っているものは、すべて「りんご３個」をコピーしたもの、すなわち、すべて同じものです（なぜなら「３×２」も「３×３」も「３×」だからです）。

だから、「３×２＋３×３」「３×５」としても差し支えはないですよね。

ここがわかれば、あとはかんたんです。

問題に戻ります。
「〇×２＋〇×３＝１５」を解くのでした。

「〇×２は、りんごが〇個で、それを２回コピーする」という意味でした。
「〇×３は、りんごが〇個で、それを３回コピーする」という意味でした。
これらを「＋」するので、つぎのようにできますよね。
※〇はいくつかわからないという意味で「？」にしています。

先ほどの話を思い出してください。
〇が５つあるので、「〇×５」にできますね。
よって、「〇×５＝１５」となります。
あとは先ほどの方程式と同じです。

「〇」はすべて同じなので、「もし〇が１だったとしたら」から考えます。

＜〇が１の場合＞
〇はすべて同じなので、〇はすべて１です。合計で５ですね。いま、全部で１５なので、〇は１ではありません。

＜〇が２の場合＞
〇はすべて同じなので、〇はすべて２です。合計で１０ですね。いま、全部で１５なので、〇は１ではありません。

＜〇が３の場合＞
〇はすべて同じなので、〇はすべて３です。合計で１５ですね。いま、全部で１５なので、〇は３です。

ここでは、これ以上は勉強しませんが、かけ算はコピー機と考えれば、変数もかんたんに理解できるのをわかっていただけたのではないでしょうか。

・「やりなおし中学数学（算数の復習編）」のトップページ
・「楽しみながら、算数・数学を勉強しよう！」のトップページ