相当算の教えかた(親向け)
つぎの問題を考えてみてください。
(例)ヒモがある。このうち、3分の1を切ったら、残りは24cmになった。ヒモの長さは?
図にすると、以下ですよね。
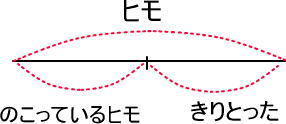
ここから、どのように解いていけばいいのでしょうか。
3つの方法があります。
1.数学の解法(□やxでおく)
2.算数の解法1(全体を1とおく)
3.算数の解法2(全体を最小公倍数とおく)
具体的にどのように教えていけばいいのでしょうか。
また、どのような欠点があるのでしょうか。
1つずつ説明していきます。
スポンサード リンク
数学の解法(□やxでおく)
まずは、数学の解法です。
わからないものを□やxでおきます。
中学受験を経験したことがなく、数学だけを勉強をしてきたかたには馴染みのある方法ですね。
数学の解法の詳細
1.(方針)ヒモの長さを□とおきます。
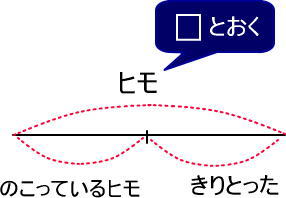
2.(埋められるところは埋めていく)つぎのようになります。
※説明は省略
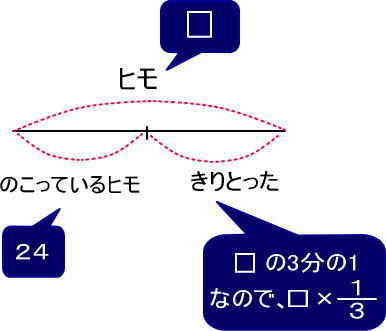
3.(計算)方程式を解きます。
あとは「□−□×(3分の1)=24」を解けば答えがでます。
数学の解法の欠点
この方法ですが、つぎの欠点があります。
・□やxがわかりにくい
理解できないわけではないですが、小学生には変数は難しく感じるようです。
具体的には、まずは、上記1の「わからないところを変数でおく」ところがひっかかります。
つぎに、上記2の「□×(3分の1)」のところもひっかかります。
・方程式が解けない
小学生にとっては「左辺と右辺が等しい」「左辺と右辺の両方を同じ数でかけたり割ったりしてもいい」のような数学的な考えかたはわかりにくいようです。よって、「□−□×(3分の1)=24」は解けません。
ちなみに、小学生とはいえ、いずれも中学数学を教え込めばできるようになります。
ただ、中学受験の算数は、方程式を使わなくても解けるので、中学数学の勉強に時間を費やすよりも、ほかの勉強に時間を割いたほうが有効です。
算数の解法(全体を1とおく)
「全体を1とおく」は、算数の解法の1つです。
受験算数を勉強したことがあるかたには馴染みのある方法だと思いますが、数学から勉強をはじめたかたは面を食らうかもしれません。
全体を1とおく方法の詳細
1.全体を「1」とおきます。
※長さなどと区別するために「まるいち(環境依存文字なのでひらがなにしています)」とします。
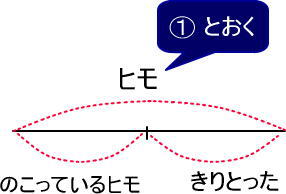
2.(埋められるところは埋めていく)つぎのようになります。
※説明は省略
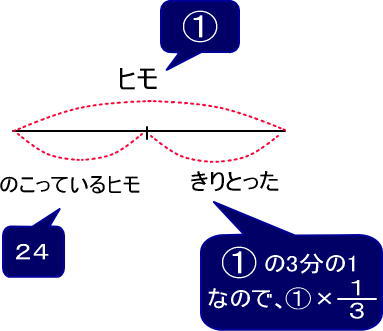
3.(計算)2/3が24なので、答えを出せます。
全体を1とおく方法の長所と短所
まずは、長所です。
・上記1は全体を1とおくだけなので小学生にもわかりやすい。
・上記2は数字と同じ感覚なので、小学生にもわかりやすい。
つぎに短所です。
・上記3の計算が分数なのでややこしい。
簡単な問題なので、まだ計算はできますが、難しくなると分数の計算が複雑になって解きにくくなります。
算数の解法(全体を最小公倍数とおく)
全体を1とおく方法だと立式のあとの計算がややこしくなるのは前述の通りです。それを回避できる方法です。
全体を最小公倍数とおく方法の長所と短所
まずは、長所です。
1.上記2の線分図は描きやすい
2.数字と同じ感覚で計算できるので、計算もわかりやすい
つぎに短所です。
・上記1の「あとのことを考えて、最初に最小公倍数を考える」が、かなりわかりにくい。
演習をこなせばすぐに慣れますが、最初のうちはわかりにくいようです。
全体を最小公倍数でおく方法がお勧め!
相当算の3つの解きかたを紹介しました。
数学しか勉強してこなかったひとは、1の方程式で解く方法を子どもに教えてしまうと思います。
しかし、子どもにとっては難しく感じますし、数学的な解きかただとなかなか解けない問題もあります。
全体を最小公倍数でおく方法がお勧めです。
※ちなみに、消去算のように数学的な解法を知っているほうが有利なところもあります。