比は「袋」で考えよう!
リンゴごを持っていたので、つぎのように、たろうくんと、はなこさんにあげました。
・たろうくんには、リンゴ2個
・はなこさんには、リンゴ3個
図にすると、つぎのようになりますよね。
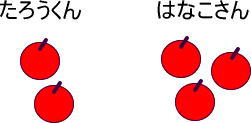
リンゴはまだまだあります。
たろうくんと、はなこさんに、もっとリンゴをあげようと思いますが、どのようにリンゴを渡していけばいいと思いますか。
いろいろな方法が考えられますよね。
たとえば、つぎの図。
たろうくんに1個、はなこさんに2個のリンゴをあげる方法です。
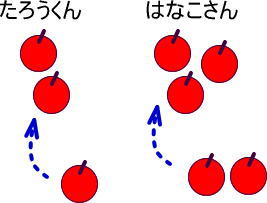
ほかにも、たろうくんに10個、はなこさんに1個のリンゴをあげる方法もあります。
それ以外にも、たろうくんに100個、はなこさんに200個リンゴをあげる方法もあります。
さて、ここでリンゴを「袋」にいれて渡していく方法を考えてみます。
具体的には、リンゴをつぎのように袋にいれて、2人に渡していく方法です。
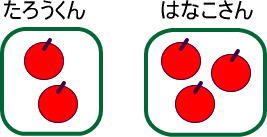
リンゴの数はどのように増えていくと思いますか。
袋が増えていくので、つぎのようになりますね。
<2袋>
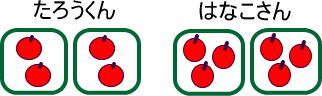
→たろうくんはリンゴ4個、はなこさんはリンゴ6個
<3袋>
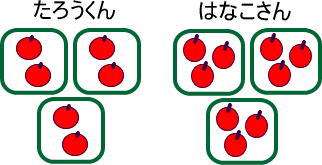
→たろうくんはリンゴ6個、はなこさんはリンゴ9個
<4袋>
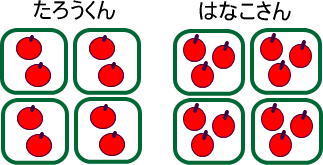
→たろうくんはリンゴ8個、はなこさんはリンゴ12個
リンゴの増えかたを見てみてください。
たろうくんが2個増えたら、はなこさんは3個リンゴが増えるのがわかると思います。
※袋に入れているので、当たり前ですね。
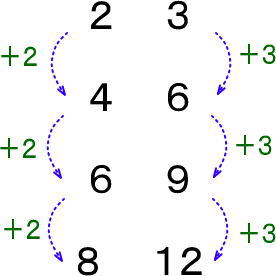
このように片方が増えると、もう片方も同じように増えるとき、つぎのように「:」で表します。
※減るときも同じです。
※大ざっぱすぎますが、いまのところは、このくらいの理解で構いません。
「2:3」
「4:6」
「6:9」
「8:12」
はじめのうちは「:は、袋にいれて考えるよー」というマークだと覚えていただいても構いません。
スポンサード リンク
スポンサード リンク
「=」でつなげる場合、つないではいけない場合
質問です。
つぎのどちらが正しいと思いますか。
(1)「1:3=2:6」
(2)「1:3=2:5」
まずは(1)です。
「1:3=2:6」の「2:6」を図で表してみました。
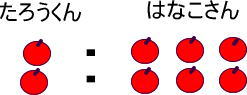
リンゴ2個を袋に入れます。
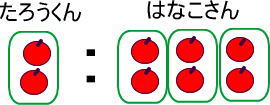
袋を手で隠すと「1:3」になりますね。
「1:3=2:6」となります。
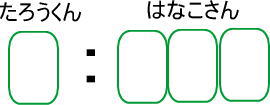
よって、答えは(2)ですが、(2)を見てみましょう。
「1:3=2:5」の「2:5」を図で表してみました。
これはどうやっても「1:3」で分けられないですよね。
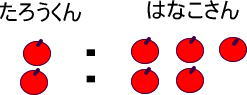
というわけで、「1:3=2:5」は間違いです。
さて、ここで、つぎの図を見てください。
(1)の「1:3=2:6」を図にしたものですが、たろうくんのリンゴの数は「×2」、はなこさんのリンゴの数も「×2」になっているのがわかりますよね。
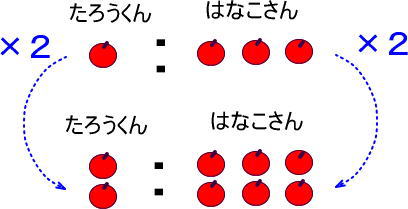
一方、(2)の「1:3=2:5」は、たろうくんのリンゴの数は「×2」ですが、はなこさんのリンゴの数は「×2」ではありません。
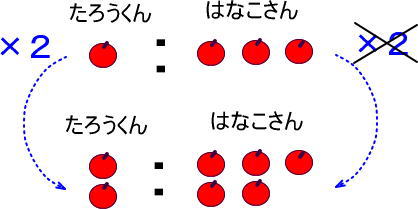
片一方が2倍になれば、もう片一方も2倍になるとき、「=」でつなげられることがわかります。
※大ざっぱですが、いまはそのように覚えておいてください。
質問です。
つぎのどちらが正しいと思いますか。
(1)「2:3=8:10」
(2)「2:3=8:12」
(1)ですが、「2→8」は「×4」ですね。「3→10」も「×4」にならないといけないので、これは間違いです。
(2)ですが、「2→8」は「×4」ですね。「3→12」も「×4」です。
よって、答えは(2)です。
「袋」で増やしたり、減らしたりするとき、不思議な関係がある1
先ほど、つぎのように袋にリンゴをいれて、袋で増やしていきました。
「2:3」
「4:6」
「6:9」
「8:12」
「2:3」と「4:6」を見比べてみましょう。
たろうくんの袋の数は「1袋」から「2袋」になっています。つまり「×2」ですね。
はなこさんの袋の数も「1袋」から「2袋」になっているので、「×2」です。
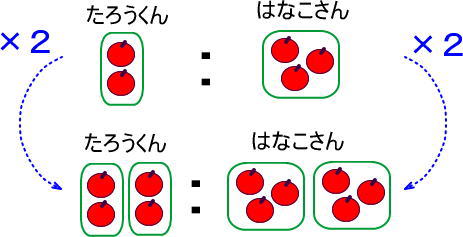
ちなみに、リンゴの数で考えても同じです。
たろうくんのリンゴの数は「2個」から「4個」になっています。つまり「×2」ですね。
はなこさんのリンゴの数も「3個」から「6個」になっているので、「×2」です。
というわけで、「2:3=4:6」です。
つぎに「2:3」と「6:9」を見比べてみましょう。
たろうくんの袋の数は「1袋」から「3袋」になっています。つまり「×3」ですね。
はなこさんの袋の数も「1袋」から「3袋」になっているので「×3」です。
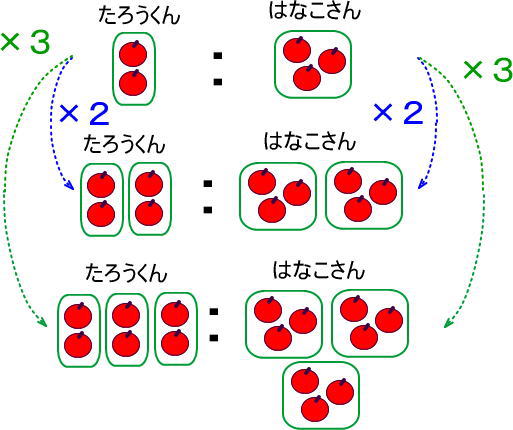
ちなみに、リンゴの数で考えても同じです。
たろうくんのリンゴの数は「2個」から「6個」になっています。つまり「×3」ですね。
はなこさんのリンゴの数も「3個」から「9個」になっているので、「×3」です。
というわけで、「2:3=6:9」です。
まとめると、図のようになります。
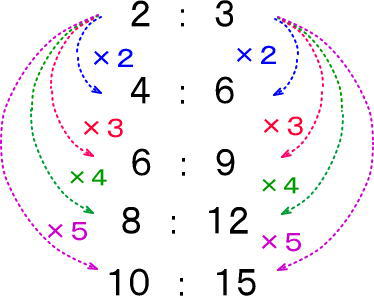
つまり、つぎのようにもできますよね。
2:3=4:6
2:3=6:9
2:3=8:12
「同じ」なので、つぎのようにもできます。
4:6=6:9
4:6=8:12
6:9=8:12
見方を変えると、たとえば、つぎのようにもできます。
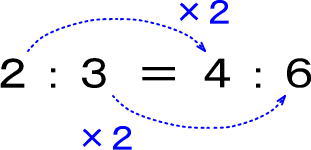
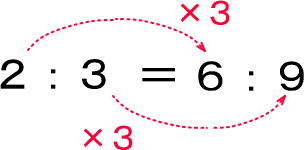
このように、袋にいれて、袋ごと増やしたり減らしたりしたもの、すべて「=」でつなぐことができます。しっかり覚えておきましょう。
比の練習問題を解いてみよう!
つぎの問題を解いてください。
比をかんたんにしてください。
(問)8:2
「:」でつながっているとき、両方の数字を同じ数でかけても、わってもいいのですよね。
だから、両方の数字を「2」でわってみます。
(8÷2):(2÷2)=4:1
「4」と「1」。
これ以上、同じ数で、わることはできませんね。
このように、これ以上、わることができないようにすることを「比をかんたんにする」といいます。
では、問題を解いてみましょう。
比をかんたんにしてください。
(1)3:12
(2)4:6
(1)両方を「3」で、わります。
(3÷3):(12÷3)=1:4
(2)両方を「2」で、わります。
(4÷2):(6÷2)=2:3