素因数分解には「はしご算」

１８、２４など、桁数が少ないと、かんたんに素因数分解できます。
しかし、２８２３のように桁数が多いと、すこし苦労するので「はしご算」を使うといいでしょう。
どのようにすればいいのでしょうか。
問を通して、はしご算のやりかたを紹介します。

（問）１０８を「はしご算」を使って素因数分解してみましょう。

（１）まずは、素因数分解する数を紙に書きます。

（２）（１）の数字に、わり算の「逆」の線を書きます。

（３）素数を思い出します。２、３、９など、いくつか思いつくはずです。まずは、これらのうち、一番ちいさな素数で１０８を割れるかどうか考えます。
一番ちいさな素数は２ですよね。１０８は２で割れるので、つぎのように書きます。

（４）１０８を（３）の数で割ります。つまり１０８を２で割るわけですね。わり算の結果をその下に書きます。これはわり算と同じです（わり算を逆にしただけ）。

（５）（４）の計算結果（今の場合は５４）にも、わり算の「逆」の線を書きます。

（６）（３）とまったく同じことをします。素数を思い出します。それらのうち、一番ちいさな素数で５４を割れるかどうか考えます。
一番ちいさな素数は２ですよね。５４は２で割れるので、つぎのように書きます。

（７）（６）の計算結果（今の場合は２７）を下に書きます。

（８）２７にも、わり算の逆の線を書きます。

（９）（３）とまったく同じことをします。素数を思い出します。それらのうち、一番ちいさな素数で２７を割れるかどうか考えます。
一番ちいさな素数は２ですよね。しかし、２７は２で割れません。

（１０）（９）のように割れない場合は、つぎの2つの条件の両方ともにあう素数を書きます。

・今までの手順で使ってきた素数（今の場合は２）よりも大きな素数
・計算結果の数（今の場合は２７）を割ることができる素数

３ですね。

（１１）２７を３で割ります。これは今までの手順と同じです。

（１２）わり算と逆の線を書きます。

（１３）９は３で割れるので、３を書きます。

（１４）９を３で割った結果を下に書きます。これ以上、割ることができないので、終わりです（まだ３で割ることができますが、１になるまで割る必要はありません）。

（１５）図の部分をかけ算にしたものが答えです。今の場合だと「２×２×３×３×３」ですね（実際は累乗の形にしてください）。

スポンサードリンク

素因数分解で間違えないようにするコツ

素因数分解するには、常にどの数だと割り切れるのかを考える必要があります。

たとえば、つぎのシーン。
108を割れる素数は何なのか考える必要に迫られます。

つぎに、つぎのシーン。
27を割れる素数は何なのかを考える必要に迫られます。

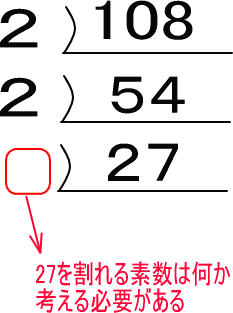
ちいさな順から素数で割っていけばいいのですが、はじめのうちは「抜け」があって、間違えてしまうことがあります。
そこで、素数を「左から順」「小さな順」で紙に書きましょう。

（例）2、3、5、7、11、13…

慣れてくれば「割り切れるかどうかを判断する方法」などで、どの素数だと割れるのかを判断すればいいでしょう。

ちなみに、たいてい、２、３、５で割ることができますが、「１２１」のように、一見すると割り切れる素数がないように見えるものもあります。
このような場合は、「１１の２乗が１２１」のように別のところで覚える知識があれば、対処できます。

スポンサードリンク

素因数分解してみよう！

（問）はしご算を使って、つぎの数を素因数分解してみましょう。

１．６
２．１８
３．３６
４．３０
５．２０
６．７２
７．１００
８．１４
９．１０５
１０．９１

解答です。
※実際は、累乗の形にしてください。ネットでは累乗にしにくいのでかけ算の形にしているだけです。

１．２×３
２．２×３×３
３．２×２×３×３
４．２×３×５
５．２×２×５
６．２×２×２×３×３
７．２×２×５×５
８．２×７
９．３×５×７
１０．７×１３（２、３、５と小さな素数で割っていっても割り切れません。そこで、ためしに7で割ると、割り切れるとわかります）

・「やりなおし中学数学（中学校三年生編）」のトップページ
・「楽しみながら、算数・数学を勉強しよう！」のトップページ