余りがある割り算
※オリジナルの解説法なので、このページをはじめて見たかたは、まずは前のページにある「わり算」から読んでください。
「9÷4」を計算してみてください。
割り算は「□×4=9」を考えればいいのでした。
しかし、つぎのようになります。
・□が2なら、4×2=8
・□が3なら、4×3=12
→9にならない!
中学数学では、このような場合、分数を使います。
しかし、算数では「あまり」を使うことがあるので、ここでは「あまり」の考え方を紹介します。
さて、先ほど□を計算しました。
□が2とは、どういうことなのでしょうか。
<□が2の場合>
・「□が2」は「9÷4の答えが2」ということ。9を等しく4つで分けたら2個ずつだったということ。
図にすると、つぎのようになります。
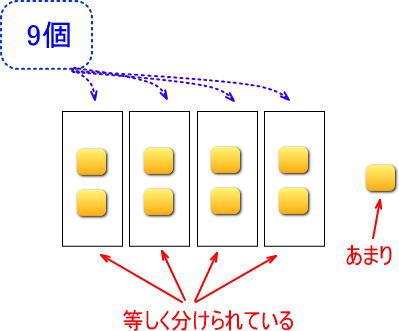
等しく分けられていますが、1個あまります。
つぎに、□が3とは、どういうことなのでしょうか。
<□が3の場合>
・「□が3」は「9÷4の答えが3」ということ。9を等しく4つで分けたら3個ずつだったということ。
図にすると、つぎのようになります。
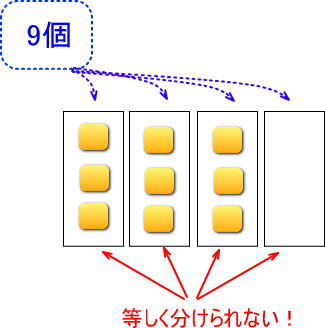
等しく分けるには足りません。
まとめます。
・9÷4だから、□×4=9を考えた。□=2だと4×2=8、□=3だと4×3=12で、ちょうど9になるのがなかった
・□=2、□=3とは、どういうことなのか考えた
・もし□が2ならば、1個、余るけど、等しく分けられた
・もし□が3ならば、等しく分けることができなかった。わり算なので等しく分けられないのはダメ
わり算なので、等しく分けられないのはダメです。そこで、□=2としますが、つぎのように余った分もついでに書きます。
9÷4=2・・・1
では、類題を解いてみましょう。
(問)「11÷3」を計算してください。
□×3=11になる□を考えます。
□が3だと9です。
□が3ということは、11を等しく3つの箱にいれると3つずつ入れるということです。3つずつ分けると9で済みます。つまり、11−9=2余ります。
□が4だと12です。
□が4ということは、11を等しく3つの箱にいれると4つずつ入れるということです。4つずつ分けると12必要です。1つ足りません。
というわけで、答えです。
11÷3=3・・・2
(問)「17÷5」を計算してください。
□が3だと15です。
□が3ということは、17を等しく5つの箱にいれると3つずつ入れることです。3つずつ分けると15で済みます。つまり、17−15=2余ります。
よって、「17÷5=3・・・2」です。