わり算の計算は、かけ算がわかっていれば、かんたん!
(問)「24÷3」を計算してみよう!
24÷3は、おはじき24個を等しく3つに分けるという意味でした。
これを図にすると、つぎのようになりましたね。
※もしこの図がわからないようであれば、前のページに戻って復習してください。
この図、どこかで見たことがありませんか。
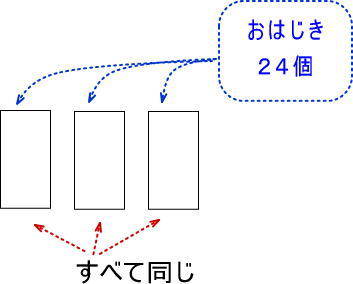
つぎの絵を見れば、思い出すのではないでしょうか。
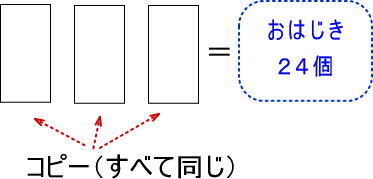
かけ算の図ですね。
おはじきのカタマリを3回コピーすれば、ぜんぶで、おはじきが24個になったという図です。
※この図がわからないならば、かけ算のページを復習しましょう。
つまり、わり算とかけ算は、図が同じなのです。
かけ算の図から、おはじきはいくつなのか考えていきましょう。
どのように考えればよかったですか。
忘れたひとに向けて、順を追って説明します。
1.おはじきは1個だったとします。それを3回コピーするわけなので、つぎの図のようになりますね。
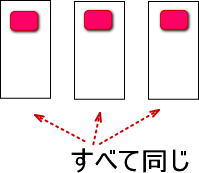
おはじきは、ぜんぶで1×3=3個となります。
しかし、いま、おはじきは、ぜんぶで24個あるので、1ではありません。
2.おはじきは2個だったとします。それを3回コピーするわけなので、つぎの図のようになりますね。
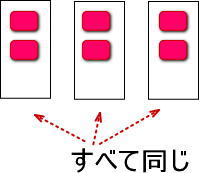
おはじきは、ぜんぶで、2×3=6個となります。
しかし、いま、おはじきは、ぜんぶで24個あるので、2ではありません。
3.おはじきが3個とします。これを3回コピーするわけなので、おはじきは、ぜんぶで3×3=9個になります。
しかし、いま、おはじきは、ぜんぶで24個あるので、3ではありません。
4.このように、おはじき1個の場合、2個の場合、3個の場合と考えていくと
、いつかわかりますが、時間がかかります。
そこで、おはじきが□個あったと考えます。
・おはじきが1個の場合。3回コピーするので、おはじきの数はぜんぶで以下。
1×3=3
・おはじきが2個の場合。3回コピーするので、おはじきの数はぜんぶで以下。
2×3=6
・おはじきが3個の場合。3回コピーするので、おはじきの数はぜんぶで以下。
3×3=9
・おはじきが□個の場合。3回コピーするので、おはじきの数はぜんぶで以下。
「?」
『?』は、□×3ですね。
これが24個になるので、□×3=24 です。
これは、かけ算が完全ならば、瞬時に□=8とわかります。
※もし、瞬時に答えがわからなかったら、かけ算のページを復習してください。
つまり、つぎのようになるわけですね。
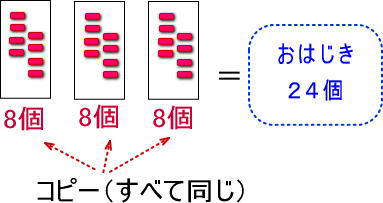
一番はじめの図に戻ります。
24÷3のイメージ図を描きました。
具体的には、「おはじき24個を等しく3つに分けた絵」を描いたのですが、それを見ていると、「あ、かけ算と同じじゃないか!」と気がつきました。
かけ算の図で考えたら、24÷3=8と、わかりました。
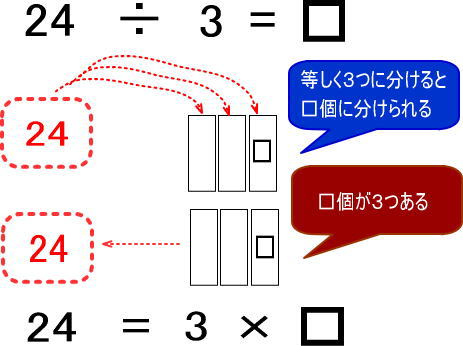
この流れを、まとめると下図になります。
わからないところがあれば、先ほどまでの説明をもう一度読み返してください。
類題です。
(問)「36÷4」はいくつでしょうか。
「おはじき36個を等しく4つに分ける」ので、図にするとつぎのようになります。
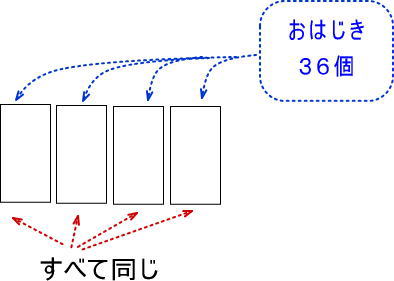
これは、かけ算と同じ図でした。
そこで、つぎのように考えるのでした。
<考えかた>
・おはじきが1個なら、4回コピーするので、おはじきは、ぜんぶで1×4=4。いま、おはじきは36個なので、これはちがう。
・おはじきが2個なら、4回コピーするので、おはじきは、ぜんぶで2×4=8。いま、おはじきは36個なので、これはちがう。
・おはじきが3個なら、4回コピーするので、おはじきは、ぜんぶで3×4=12。いま、おはじきは36個なので、これはちがう。
・おはじきが□つなら、4回コピーするので、おはじきは、ぜんぶで□×4=□×4。いま、おはじきが36個。
よって「□×4=36」「□=9」。
答えは「36÷4=9」。
ここの壁を越えれば、わり算の計算はできるようになります。