わり算は「ナイフを使って等しく分ける」イメージ！
「６÷２＝３」は、どういう意味だと思いますか。
つぎのように考えます。
・「６」は、おはじきの数
・「÷２」は、ナイフを使って、等しく２つに分ける
図にすると、つぎのようになります。
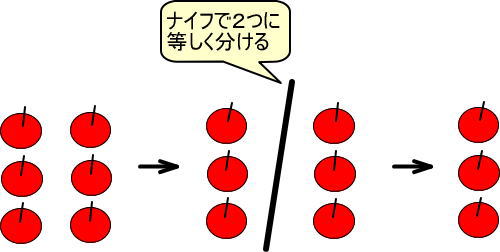
式でいうと、つぎのようになります。
どうでしょうか。
イメージできたでしょうか。
では、問題です。
「６÷３＝２」は、どういう図や式になると思いますか。
考えてみてください。
さて、答えですが、図はつぎのようになりますね。
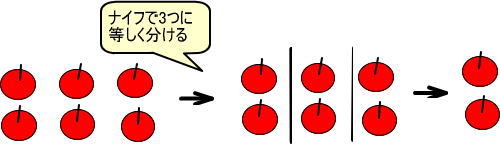
式は、つぎのようになりますね。
では、問題です。
「４÷２＝２」は、どういう図や式になると思いますか。
考えてみてください。
まずは、図ですが、つぎのようになりますね。
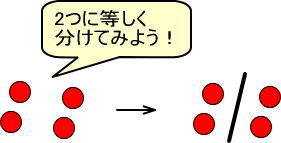
式は、つぎのようになりますね。
【まとめ】「▲÷●」を見たら、つぎのように考えよう
・おはじきが▲個ある
・そのおはじきをナイフを使って●つに等しく分ける
スポンサード リンク
わり算のイメージを確たるものにするために、考えよう！
つぎの問を解いてください。
（問）おはじきが８個ありました。これを□つに等しくわけたら、△個になりました。□と△は、いくつだと思いますか。
まずは、つぎのようにできますね。
８個のおはじきを２つに等しくわけたら、４個になったわけなので、□は２、△は４です。
これ以外にも、別の分けかたがありますよね。
つぎのようにもできます。
８個のおはじきを４つに等しくわけたら、２個になったわけなので、□は４、△は２です。
数学の世界では「１つで等しく分ける」とも考えますね。
８個のおはじき１つに等しくわけたら、８個になったわけなので、□は１、△は８です。
「なんか変…」と思う気持ち、よくわかりますが、そのうち慣れてきます。
スポンサード リンク
割り切れないケースもある
（問）おはじきが３つあります。２つに等しく分てください。
しかし、つぎのように等しく分けられません。
このように「等しく分けられないケース」もあります。
なお、等しく分けられない場合は「分数」や「あまり」を使います。それらについては、今後のレッスンで扱います。
（問）おはじきを１０個を等しく２つに分けてください。その後、等しく３つに分けてください。
等しく２つに分けると、つぎのように分けられますね。
しかし、等しく３つでは分けられません。
「等しく２つで分けられたのに、等しく３つでは分けられない」ようなケースもあることを知っておいてください。